/* QuadCurve2D.java -- represents a parameterized quadratic curve in 2-D space
Copyright (C) 2002, 2003 Free Software Foundation
This file is part of GNU Classpath.
GNU Classpath is free software; you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation; either version 2, or (at your option)
any later version.
GNU Classpath is distributed in the hope that it will be useful, but
WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU
General Public License for more details.
You should have received a copy of the GNU General Public License
along with GNU Classpath; see the file COPYING. If not, write to the
Free Software Foundation, Inc., 59 Temple Place, Suite 330, Boston, MA
02111-1307 USA.
Linking this library statically or dynamically with other modules is
making a combined work based on this library. Thus, the terms and
conditions of the GNU General Public License cover the whole
combination.
As a special exception, the copyright holders of this library give you
permission to link this library with independent modules to produce an
executable, regardless of the license terms of these independent
modules, and to copy and distribute the resulting executable under
terms of your choice, provided that you also meet, for each linked
independent module, the terms and conditions of the license of that
module. An independent module is a module which is not derived from
or based on this library. If you modify this library, you may extend
this exception to your version of the library, but you are not
obligated to do so. If you do not wish to do so, delete this
exception statement from your version. */
package java.awt.geom;
import java.awt.Rectangle;
import java.awt.Shape;
import java.util.NoSuchElementException;
/**
* A two-dimensional curve that is parameterized with a quadratic
* function.
*
* 
*
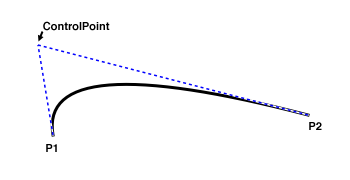* @author Eric Blake (ebb9@email.byu.edu)
* @author Graydon Hoare (graydon@redhat.com)
* @author Sascha Brawer (brawer@dandelis.ch)
*
* @since 1.2
*/
public abstract class QuadCurve2D
implements Shape, Cloneable
{
/**
* Constructs a new QuadCurve2D. Typical users will want to
* construct instances of a subclass, such as {@link
* QuadCurve2D.Float} or {@link QuadCurve2D.Double}.
*/
protected QuadCurve2D()
{
}
/**
* Returns the x coordinate of the curve’s start
* point.
*/
public abstract double getX1();
/**
* Returns the y coordinate of the curve’s start
* point.
*/
public abstract double getY1();
/**
* Returns the curve’s start point.
*/
public abstract Point2D getP1();
/**
* Returns the x coordinate of the curve’s control
* point.
*/
public abstract double getCtrlX();
/**
* Returns the y coordinate of the curve’s control
* point.
*/
public abstract double getCtrlY();
/**
* Returns the curve’s control point.
*/
public abstract Point2D getCtrlPt();
/**
* Returns the x coordinate of the curve’s end
* point.
*/
public abstract double getX2();
/**
* Returns the y coordinate of the curve’s end
* point.
*/
public abstract double getY2();
/**
* Returns the curve’s end point.
*/
public abstract Point2D getP2();
/**
* Changes the curve geometry, separately specifying each coordinate
* value.
*
* @param x1 the x coordinate of the curve’s new start
* point.
*
* @param y1 the y coordinate of the curve’s new start
* point.
*
* @param cx the x coordinate of the curve’s new
* control point.
*
* @param cy the y coordinate of the curve’s new
* control point.
*
* @param x2 the x coordinate of the curve’s new end
* point.
*
* @param y2 the y coordinate of the curve’s new end
* point.
*/
public abstract void setCurve(double x1, double y1, double cx, double cy,
double x2, double y2);
/**
* Changes the curve geometry, passing coordinate values in an
* array.
*
* @param coords an array containing the new coordinate values. The
* x coordinate of the new start point is located at
* coords[offset], its y coordinate at
* coords[offset + 1]. The x coordinate of the
* new control point is located at coords[offset + 2],
* its y coordinate at coords[offset + 3]. The
* x coordinate of the new end point is located at
* coords[offset + 4], its y coordinate at
* coords[offset + 5].
*
* @param offset the offset of the first coordinate value in
* coords.
*/
public void setCurve(double[] coords, int offset)
{
setCurve(coords[offset++], coords[offset++],
coords[offset++], coords[offset++],
coords[offset++], coords[offset++]);
}
/**
* Changes the curve geometry, specifying coordinate values in
* separate Point objects.
*
*
*
*
The curve does not keep any reference to the passed point
* objects. Therefore, a later change to p1,
* c p2 will not affect the curve
* geometry.
*
* @param p1 the new start point.
* @param c the new control point.
* @param p2 the new end point.
*/
public void setCurve(Point2D p1, Point2D c, Point2D p2)
{
setCurve(p1.getX(), p1.getY(), c.getX(), c.getY(),
p2.getX(), p2.getY());
}
/**
* Changes the curve geometry, specifying coordinate values in an
* array of Point objects.
*
*
*
*
The curve does not keep references to the passed point
* objects. Therefore, a later change to the pts array
* or any of its elements will not affect the curve geometry.
*
* @param pts an array containing the points. The new start point
* is located at pts[offset], the new control
* point at pts[offset + 1], and the new end point
* at pts[offset + 2].
*
* @param offset the offset of the start point in pts.
*/
public void setCurve(Point2D[] pts, int offset)
{
setCurve(pts[offset].getX(), pts[offset].getY(),
pts[offset + 1].getX(), pts[offset + 1].getY(),
pts[offset + 2].getX(), pts[offset + 2].getY());
}
/**
* Changes the geometry of the curve to that of another curve.
*
* @param c the curve whose coordinates will be copied.
*/
public void setCurve(QuadCurve2D c)
{
setCurve(c.getX1(), c.getY1(), c.getCtrlX(), c.getCtrlY(),
c.getX2(), c.getY2());
}
/**
* Calculates the squared flatness of a quadratic curve, directly
* specifying each coordinate value. The flatness is the distance of
* the control point to the line between start and end point.
*
*
*
*
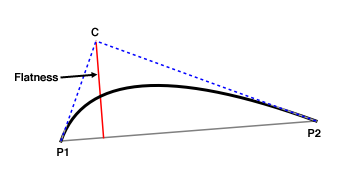In the above drawing, the straight line connecting start point
* P1 and end point P2 is depicted in gray. The result will be the
* the square of the distance between C and the gray line, i.e.
* the squared length of the red line.
*
* @param x1 the x coordinate of the start point P1.
* @param y1 the y coordinate of the start point P1.
* @param cx the x coordinate of the control point C.
* @param cy the y coordinate of the control point C.
* @param x2 the x coordinate of the end point P2.
* @param y2 the y coordinate of the end point P2.
*/
public static double getFlatnessSq(double x1, double y1, double cx,
double cy, double x2, double y2)
{
return Line2D.ptSegDistSq(x1, y1, x2, y2, cx, cy);
}
/**
* Calculates the flatness of a quadratic curve, directly specifying
* each coordinate value. The flatness is the distance of the
* control point to the line between start and end point.
*
*
*
*
In the above drawing, the straight line connecting start point
* P1 and end point P2 is depicted in gray. The result will be the
* the distance between C and the gray line, i.e. the length of
* the red line.
*
* @param x1 the x coordinate of the start point P1.
* @param y1 the y coordinate of the start point P1.
* @param cx the x coordinate of the control point C.
* @param cy the y coordinate of the control point C.
* @param x2 the x coordinate of the end point P2.
* @param y2 the y coordinate of the end point P2.
*/
public static double getFlatness(double x1, double y1, double cx, double cy,
double x2, double y2)
{
return Line2D.ptSegDist(x1, y1, x2, y2, cx, cy);
}
/**
* Calculates the squared flatness of a quadratic curve, specifying
* the coordinate values in an array. The flatness is the distance
* of the control point to the line between start and end point.
*
*
*
*
In the above drawing, the straight line connecting start point
* P1 and end point P2 is depicted in gray. The result will be the
* the square of the distance between C and the gray line, i.e.
* the squared length of the red line.
*
* @param coords an array containing the coordinate values. The
* x coordinate of the start point P1 is located at
* coords[offset], its y coordinate at
* coords[offset + 1]. The x coordinate of the
* control point C is located at coords[offset + 2],
* its y coordinate at coords[offset + 3]. The
* x coordinate of the end point P2 is located at
* coords[offset + 4], its y coordinate at
* coords[offset + 5].
*
* @param offset the offset of the first coordinate value in
* coords.
*/
public static double getFlatnessSq(double[] coords, int offset)
{
return Line2D.ptSegDistSq(coords[offset], coords[offset + 1],
coords[offset + 4], coords[offset + 5],
coords[offset + 2], coords[offset + 3]);
}
/**
* Calculates the flatness of a quadratic curve, specifying the
* coordinate values in an array. The flatness is the distance of
* the control point to the line between start and end point.
*
*
*
*
In the above drawing, the straight line connecting start point
* P1 and end point P2 is depicted in gray. The result will be the
* the the distance between C and the gray line, i.e. the length of
* the red line.
*
* @param coords an array containing the coordinate values. The
* x coordinate of the start point P1 is located at
* coords[offset], its y coordinate at
* coords[offset + 1]. The x coordinate of the
* control point C is located at coords[offset + 2],
* its y coordinate at coords[offset + 3]. The
* x coordinate of the end point P2 is located at
* coords[offset + 4], its y coordinate at
* coords[offset + 5].
*
* @param offset the offset of the first coordinate value in
* coords.
*/
public static double getFlatness(double[] coords, int offset)
{
return Line2D.ptSegDist(coords[offset], coords[offset + 1],
coords[offset + 4], coords[offset + 5],
coords[offset + 2], coords[offset + 3]);
}
/**
* Calculates the squared flatness of this curve. The flatness is
* the distance of the control point to the line between start and
* end point.
*
*
*
*
In the above drawing, the straight line connecting start point
* P1 and end point P2 is depicted in gray. The result will be the
* the square of the distance between C and the gray line, i.e. the
* squared length of the red line.
*/
public double getFlatnessSq()
{
return Line2D.ptSegDistSq(getX1(), getY1(),
getX2(), getY2(),
getCtrlX(), getCtrlY());
}
/**
* Calculates the flatness of this curve. The flatness is the
* distance of the control point to the line between start and end
* point.
*
*
*
*
In the above drawing, the straight line connecting start point
* P1 and end point P2 is depicted in gray. The result will be the
* the distance between C and the gray line, i.e. the length of the
* red line.
*/
public double getFlatness()
{
return Line2D.ptSegDist(getX1(), getY1(),
getX2(), getY2(),
getCtrlX(), getCtrlY());
}
/**
* Subdivides this curve into two halves.
*
*
*
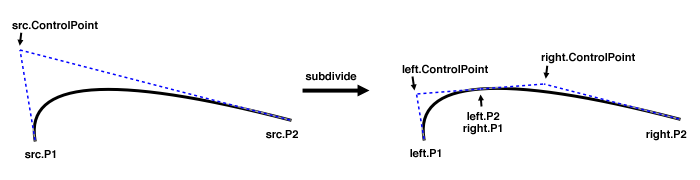* @param left a curve whose geometry will be set to the left half
* of this curve, or null if the caller is not
* interested in the left half.
*
* @param right a curve whose geometry will be set to the right half
* of this curve, or null if the caller is not
* interested in the right half.
*/
public void subdivide(QuadCurve2D left, QuadCurve2D right)
{
// Use empty slots at end to share single array.
double[] d = new double[] { getX1(), getY1(), getCtrlX(), getCtrlY(),
getX2(), getY2(), 0, 0, 0, 0 };
subdivide(d, 0, d, 0, d, 4);
if (left != null)
left.setCurve(d, 0);
if (right != null)
right.setCurve(d, 4);
}
/**
* Subdivides a quadratic curve into two halves.
*
*
*
* @param src the curve to be subdivided.
*
* @param left a curve whose geometry will be set to the left half
* of src, or null if the caller is not
* interested in the left half.
*
* @param right a curve whose geometry will be set to the right half
* of src, or null if the caller is not
* interested in the right half.
*/
public static void subdivide(QuadCurve2D src, QuadCurve2D left,
QuadCurve2D right)
{
src.subdivide(left, right);
}
/**
* Subdivides a quadratic curve into two halves, passing all
* coordinates in an array.
*
*
*
*
The left end point and the right start point will always be
* identical. Memory-concious programmers thus may want to pass the
* same array for both left and right, and
* set rightOff to leftOff + 4.
*
* @param src an array containing the coordinates of the curve to be
* subdivided. The x coordinate of the start point is
* located at src[srcOff], its y at
* src[srcOff + 1]. The x coordinate of the
* control point is located at src[srcOff + 2], its
* y at src[srcOff + 3]. The x
* coordinate of the end point is located at src[srcOff +
* 4], its y at src[srcOff + 5].
*
* @param srcOff an offset into src, specifying
* the index of the start point’s x coordinate.
*
* @param left an array that will receive the coordinates of the
* left half of src. It is acceptable to pass
* src. A caller who is not interested in the left half
* can pass null.
*
* @param leftOff an offset into left, specifying the
* index where the start point’s x coordinate will be
* stored.
*
* @param right an array that will receive the coordinates of the
* right half of src. It is acceptable to pass
* src or left. A caller who is not
* interested in the right half can pass null.
*
* @param rightOff an offset into right, specifying the
* index where the start point’s x coordinate will be
* stored.
*/
public static void subdivide(double[] src, int srcOff,
double[] left, int leftOff,
double[] right, int rightOff)
{
double x1, y1, xc, yc, x2, y2;
x1 = src[srcOff];
y1 = src[srcOff + 1];
xc = src[srcOff + 2];
yc = src[srcOff + 3];
x2 = src[srcOff + 4];
y2 = src[srcOff + 5];
if (left != null)
{
left[leftOff] = x1;
left[leftOff + 1] = y1;
}
if (right != null)
{
right[rightOff + 4] = x2;
right[rightOff + 5] = y2;
}
x1 = (x1 + xc) / 2;
x2 = (xc + x2) / 2;
xc = (x1 + x2) / 2;
y1 = (y1 + yc) / 2;
y2 = (y2 + yc) / 2;
yc = (y1 + y2) / 2;
if (left != null)
{
left[leftOff + 2] = x1;
left[leftOff + 3] = y1;
left[leftOff + 4] = xc;
left[leftOff + 5] = yc;
}
if (right != null)
{
right[rightOff] = xc;
right[rightOff + 1] = yc;
right[rightOff + 2] = x2;
right[rightOff + 3] = y2;
}
}
/**
* Finds the non-complex roots of a quadratic equation, placing the
* results into the same array as the equation coefficients. The
* following equation is being solved:
*
*
eqn[2] · x2
* + eqn[1] · x
* + eqn[0]
* = 0
*
*
* For some background about solving quadratic equations, see the
* article “Quadratic Formula” in PlanetMath. For an extensive library
* of numerical algorithms written in the C programming language,
* see the GNU Scientific
* Library.
*
* @see #solveQuadratic(double[], double[])
* @see CubicCurve2D#solveCubic(double[], double[])
*
* @param eqn an array with the coefficients of the equation. When
* this procedure has returned, eqn will contain the
* non-complex solutions of the equation, in no particular order.
*
* @return the number of non-complex solutions. A result of 0
* indicates that the equation has no non-complex solutions. A
* result of -1 indicates that the equation is constant (i.e.,
* always or never zero).
*
* @author Brian Gough
* (original C implementation in the GNU Scientific Library)
*
* @author Sascha Brawer
* (adaptation to Java)
*/
public static int solveQuadratic(double[] eqn)
{
return solveQuadratic(eqn, eqn);
}
/**
* Finds the non-complex roots of a quadratic equation. The
* following equation is being solved:
*
*
eqn[2] · x2
* + eqn[1] · x
* + eqn[0]
* = 0
*
*
* For some background about solving quadratic equations, see the
* article “Quadratic Formula” in PlanetMath. For an extensive library
* of numerical algorithms written in the C programming language,
* see the GNU Scientific
* Library.
*
* @see CubicCurve2D#solveCubic(double[],double[])
*
* @param eqn an array with the coefficients of the equation.
*
* @param res an array into which the non-complex roots will be
* stored. The results may be in an arbitrary order. It is safe to
* pass the same array object reference for both eqn
* and res.
*
* @return the number of non-complex solutions. A result of 0
* indicates that the equation has no non-complex solutions. A
* result of -1 indicates that the equation is constant (i.e.,
* always or never zero).
*
* @author Brian Gough
* (original C implementation in the GNU Scientific Library)
*
* @author Sascha Brawer
* (adaptation to Java)
*/
public static int solveQuadratic(double[] eqn, double[] res)
{
// Taken from poly/solve_quadratic.c in the GNU Scientific Library
// (GSL), cvs revision 1.7 of 2003-07-26. For the original source,
// see http://www.gnu.org/software/gsl/
//
// Brian Gough, the author of that code, has granted the
// permission to use it in GNU Classpath under the GNU Classpath
// license, and has assigned the copyright to the Free Software
// Foundation.
//
// The Java implementation is very similar to the GSL code, but
// not a strict one-to-one copy. For example, GSL would sort the
// result.
double a, b, c, disc;
c = eqn[0];
b = eqn[1];
a = eqn[2];
// Check for linear or constant functions. This is not done by the
// GNU Scientific Library. Without this special check, we
// wouldn't return -1 for constant functions, and 2 instead of 1
// for linear functions.
if (a == 0)
{
if (b == 0)
return -1;
res[0] = -c / b;
return 1;
}
disc = b * b - 4 * a * c;
if (disc < 0)
return 0;
if (disc == 0)
{
// The GNU Scientific Library returns two identical results here.
// We just return one.
res[0] = -0.5 * b / a ;
return 1;
}
// disc > 0
if (b == 0)
{
double r;
r = Math.abs(0.5 * Math.sqrt(disc) / a);
res[0] = -r;
res[1] = r;
}
else
{
double sgnb, temp;
sgnb = (b > 0 ? 1 : -1);
temp = -0.5 * (b + sgnb * Math.sqrt(disc));
// The GNU Scientific Library sorts the result here. We don't.
res[0] = temp / a;
res[1] = c / temp;
}
return 2;
}
/**
* Determines whether a point lies inside the area that is bounded
* by the curve and the straight line connecting its end points.
*
*
*
*
The above drawing illustrates in which area points are
* considered “contained” in a QuadCurve2D.
*/
public boolean contains(double x, double y)
{
// XXX Implement.
throw new Error("not implemented");
}
/**
* Determines whether a point lies inside the area that is bounded
* by the curve and the straight line connecting its end points.
*
*
*
*
The above drawing illustrates in which area points are
* considered “contained” in a QuadCurve2D.
*/
public boolean contains(Point2D p)
{
return contains(p.getX(), p.getY());
}
public boolean intersects(double x, double y, double w, double h)
{
// XXX Implement.
throw new Error("not implemented");
}
public boolean intersects(Rectangle2D r)
{
return intersects(r.getX(), r.getY(), r.getWidth(), r.getHeight());
}
public boolean contains(double x, double y, double w, double h)
{
// XXX Implement.
throw new Error("not implemented");
}
public boolean contains(Rectangle2D r)
{
return contains(r.getX(), r.getY(), r.getWidth(), r.getHeight());
}
/**
* Determines the smallest rectangle that encloses the
* curve’s start, end and control point. As the illustration
* below shows, the invisible control point may cause the bounds to
* be much larger than the area that is actually covered by the
* curve.
*
*
*/
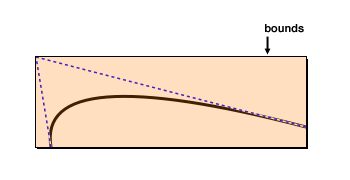public Rectangle getBounds()
{
return getBounds2D().getBounds();
}
public PathIterator getPathIterator(final AffineTransform at)
{
return new PathIterator()
{
/** Current coordinate. */
private int current = 0;
public int getWindingRule()
{
return WIND_NON_ZERO;
}
public boolean isDone()
{
return current >= 2;
}
public void next()
{
current++;
}
public int currentSegment(float[] coords)
{
int result;
switch (current)
{
case 0:
coords[0] = (float) getX1();
coords[1] = (float) getY1();
result = SEG_MOVETO;
break;
case 1:
coords[0] = (float) getCtrlX();
coords[1] = (float) getCtrlY();
coords[2] = (float) getX2();
coords[3] = (float) getY2();
result = SEG_QUADTO;
break;
default:
throw new NoSuchElementException("quad iterator out of bounds");
}
if (at != null)
at.transform(coords, 0, coords, 0, 2);
return result;
}
public int currentSegment(double[] coords)
{
int result;
switch (current)
{
case 0:
coords[0] = getX1();
coords[1] = getY1();
result = SEG_MOVETO;
break;
case 1:
coords[0] = getCtrlX();
coords[1] = getCtrlY();
coords[2] = getX2();
coords[3] = getY2();
result = SEG_QUADTO;
break;
default:
throw new NoSuchElementException("quad iterator out of bounds");
}
if (at != null)
at.transform(coords, 0, coords, 0, 2);
return result;
}
};
}
public PathIterator getPathIterator(AffineTransform at, double flatness)
{
return new FlatteningPathIterator(getPathIterator(at), flatness);
}
/**
* Creates a new curve with the same contents as this one.
*
* @return the clone.
*/
public Object clone()
{
try
{
return super.clone();
}
catch (CloneNotSupportedException e)
{
throw (Error) new InternalError().initCause(e); // Impossible
}
}
/**
* A two-dimensional curve that is parameterized with a quadratic
* function and stores coordinate values in double-precision
* floating-point format.
*
* @see QuadCurve2D.Float
*
* @author Eric Blake (ebb9@email.byu.edu)
* @author Sascha Brawer (brawer@dandelis.ch)
*/
public static class Double
extends QuadCurve2D
{
/**
* The x coordinate of the curve’s start point.
*/
public double x1;
/**
* The y coordinate of the curve’s start point.
*/
public double y1;
/**
* The x coordinate of the curve’s control point.
*/
public double ctrlx;
/**
* The y coordinate of the curve’s control point.
*/
public double ctrly;
/**
* The x coordinate of the curve’s end point.
*/
public double x2;
/**
* The y coordinate of the curve’s end point.
*/
public double y2;
/**
* Constructs a new QuadCurve2D that stores its coordinate values
* in double-precision floating-point format. All points are
* initially at position (0, 0).
*/
public Double()
{
}
/**
* Constructs a new QuadCurve2D that stores its coordinate values
* in double-precision floating-point format, specifying the
* initial position of each point.
*
* @param x1 the x coordinate of the curve’s start
* point.
*
* @param y1 the y coordinate of the curve’s start
* point.
*
* @param cx the x coordinate of the curve’s control
* point.
*
* @param cy the y coordinate of the curve’s control
* point.
*
* @param x2 the x coordinate of the curve’s end
* point.
*
* @param y2 the y coordinate of the curve’s end
* point.
*/
public Double(double x1, double y1, double cx, double cy,
double x2, double y2)
{
this.x1 = x1;
this.y1 = y1;
ctrlx = cx;
ctrly = cy;
this.x2 = x2;
this.y2 = y2;
}
/**
* Returns the x coordinate of the curve’s start
* point.
*/
public double getX1()
{
return x1;
}
/**
* Returns the y coordinate of the curve’s start
* point.
*/
public double getY1()
{
return y1;
}
/**
* Returns the curve’s start point.
*/
public Point2D getP1()
{
return new Point2D.Double(x1, y1);
}
/**
* Returns the x coordinate of the curve’s control
* point.
*/
public double getCtrlX()
{
return ctrlx;
}
/**
* Returns the y coordinate of the curve’s control
* point.
*/
public double getCtrlY()
{
return ctrly;
}
/**
* Returns the curve’s control point.
*/
public Point2D getCtrlPt()
{
return new Point2D.Double(ctrlx, ctrly);
}
/**
* Returns the x coordinate of the curve’s end
* point.
*/
public double getX2()
{
return x2;
}
/**
* Returns the y coordinate of the curve’s end
* point.
*/
public double getY2()
{
return y2;
}
/**
* Returns the curve’s end point.
*/
public Point2D getP2()
{
return new Point2D.Double(x2, y2);
}
/**
* Changes the geometry of the curve.
*
* @param x1 the x coordinate of the curve’s new
* start point.
*
* @param y1 the y coordinate of the curve’s new
* start point.
*
* @param cx the x coordinate of the curve’s new
* control point.
*
* @param cy the y coordinate of the curve’s new
* control point.
*
* @param x2 the x coordinate of the curve’s new
* end point.
*
* @param y2 the y coordinate of the curve’s new
* end point.
*/
public void setCurve(double x1, double y1, double cx, double cy,
double x2, double y2)
{
this.x1 = x1;
this.y1 = y1;
ctrlx = cx;
ctrly = cy;
this.x2 = x2;
this.y2 = y2;
}
/**
* Determines the smallest rectangle that encloses the
* curve’s start, end and control point. As the
* illustration below shows, the invisible control point may cause
* the bounds to be much larger than the area that is actually
* covered by the curve.
*
*
*/
public Rectangle2D getBounds2D()
{
double nx1 = Math.min(Math.min(x1, ctrlx), x2);
double ny1 = Math.min(Math.min(y1, ctrly), y2);
double nx2 = Math.max(Math.max(x1, ctrlx), x2);
double ny2 = Math.max(Math.max(y1, ctrly), y2);
return new Rectangle2D.Double(nx1, ny1, nx2 - nx1, ny2 - ny1);
}
}
/**
* A two-dimensional curve that is parameterized with a quadratic
* function and stores coordinate values in single-precision
* floating-point format.
*
* @see QuadCurve2D.Double
*
* @author Eric Blake (ebb9@email.byu.edu)
* @author Sascha Brawer (brawer@dandelis.ch)
*/
public static class Float
extends QuadCurve2D
{
/**
* The x coordinate of the curve’s start point.
*/
public float x1;
/**
* The y coordinate of the curve’s start point.
*/
public float y1;
/**
* The x coordinate of the curve’s control point.
*/
public float ctrlx;
/**
* The y coordinate of the curve’s control point.
*/
public float ctrly;
/**
* The x coordinate of the curve’s end point.
*/
public float x2;
/**
* The y coordinate of the curve’s end point.
*/
public float y2;
/**
* Constructs a new QuadCurve2D that stores its coordinate values
* in single-precision floating-point format. All points are
* initially at position (0, 0).
*/
public Float()
{
}
/**
* Constructs a new QuadCurve2D that stores its coordinate values
* in single-precision floating-point format, specifying the
* initial position of each point.
*
* @param x1 the x coordinate of the curve’s start
* point.
*
* @param y1 the y coordinate of the curve’s start
* point.
*
* @param cx the x coordinate of the curve’s control
* point.
*
* @param cy the y coordinate of the curve’s control
* point.
*
* @param x2 the x coordinate of the curve’s end
* point.
*
* @param y2 the y coordinate of the curve’s end
* point.
*/
public Float(float x1, float y1, float cx, float cy,
float x2, float y2)
{
this.x1 = x1;
this.y1 = y1;
ctrlx = cx;
ctrly = cy;
this.x2 = x2;
this.y2 = y2;
}
/**
* Returns the x coordinate of the curve’s start
* point.
*/
public double getX1()
{
return x1;
}
/**
* Returns the y coordinate of the curve’s start
* point.
*/
public double getY1()
{
return y1;
}
/**
* Returns the curve’s start point.
*/
public Point2D getP1()
{
return new Point2D.Float(x1, y1);
}
/**
* Returns the x coordinate of the curve’s control
* point.
*/
public double getCtrlX()
{
return ctrlx;
}
/**
* Returns the y coordinate of the curve’s control
* point.
*/
public double getCtrlY()
{
return ctrly;
}
/**
* Returns the curve’s control point.
*/
public Point2D getCtrlPt()
{
return new Point2D.Float(ctrlx, ctrly);
}
/**
* Returns the x coordinate of the curve’s end
* point.
*/
public double getX2()
{
return x2;
}
/**
* Returns the y coordinate of the curve’s end
* point.
*/
public double getY2()
{
return y2;
}
/**
* Returns the curve’s end point.
*/
public Point2D getP2()
{
return new Point2D.Float(x2, y2);
}
/**
* Changes the geometry of the curve, specifying coordinate values
* as double-precision floating-point numbers.
*
* @param x1 the x coordinate of the curve’s new
* start point.
*
* @param y1 the y coordinate of the curve’s new
* start point.
*
* @param cx the x coordinate of the curve’s new
* control point.
*
* @param cy the y coordinate of the curve’s new
* control point.
*
* @param x2 the x coordinate of the curve’s new
* end point.
*
* @param y2 the y coordinate of the curve’s new
* end point.
*/
public void setCurve(double x1, double y1, double cx, double cy,
double x2, double y2)
{
this.x1 = (float) x1;
this.y1 = (float) y1;
ctrlx = (float) cx;
ctrly = (float) cy;
this.x2 = (float) x2;
this.y2 = (float) y2;
}
/**
* Changes the geometry of the curve, specifying coordinate values
* as single-precision floating-point numbers.
*
* @param x1 the x coordinate of the curve’s new
* start point.
*
* @param y1 the y coordinate of the curve’s new
* start point.
*
* @param cx the x coordinate of the curve’s new
* control point.
*
* @param cy the y coordinate of the curve’s new
* control point.
*
* @param x2 the x coordinate of the curve’s new
* end point.
*
* @param y2 the y coordinate of the curve’s new
* end point.
*/
public void setCurve(float x1, float y1, float cx, float cy,
float x2, float y2)
{
this.x1 = x1;
this.y1 = y1;
ctrlx = cx;
ctrly = cy;
this.x2 = x2;
this.y2 = y2;
}
/**
* Determines the smallest rectangle that encloses the
* curve’s start, end and control point. As the
* illustration below shows, the invisible control point may cause
* the bounds to be much larger than the area that is actually
* covered by the curve.
*
*
*/
public Rectangle2D getBounds2D()
{
float nx1 = (float) Math.min(Math.min(x1, ctrlx), x2);
float ny1 = (float) Math.min(Math.min(y1, ctrly), y2);
float nx2 = (float) Math.max(Math.max(x1, ctrlx), x2);
float ny2 = (float) Math.max(Math.max(y1, ctrly), y2);
return new Rectangle2D.Float(nx1, ny1, nx2 - nx1, ny2 - ny1);
}
}
}